Published in: the Review of Economic Studies, 84(7), July 2020 (pp. 1989-2018)
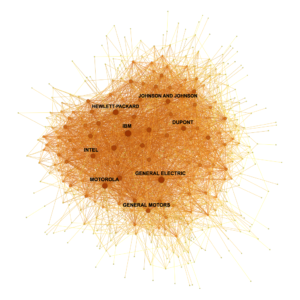
Abstract. In this article, I directly test the hypothesis that interactions between inventors of different firms drive knowledge spillovers. I construct a network of publicly traded companies in which each link is a function of the relative proportion of two firms’ inventors who have former patent collaborators in both organizations. I use this measure to weigh the impact of R&D performed by each firm on the productivity and innovation outcomes of its network linkages. An empirical concern is that the resulting estimates may reflect unobserved, simultaneous determinants of firm performance, network connections, and external R&D. I address this problem with an innovative IV strategy, motivated by a game-theoretic model of firm interaction. I instrument the R&D of one firm’s connections with that of other firms that are sufficiently distant in network space. With the resulting spillover estimates, I calculate that among firms connected to the network the marginal social return of R&D amounts to approximately 112% of the marginal private return.
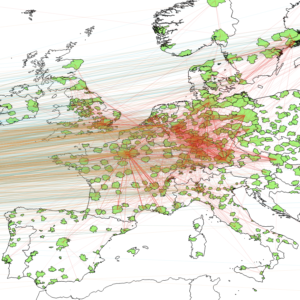Abstract. In this paper I examine episodes in which superstar inventors relocate to a new city. In particular, in order to assess whether the beneficial effects of physical proximity to a superstar have a restricted network dimension or a wider spatial breadth (spillovers), I estimate changes in patterns of patenting activity following these events for two different groups of inventors: the superstar’s close collaborators, and all the other inventors in a given urban area, for both the locality where the superstar moves to and for the one that is left behind. In the case of collaborators, I restrict the attention to patents realized independently from the superstar. The results from the event study register a large and persistent positive effect on the collaborators in the city of destination, as well as a simultaneous negative trend affecting those still residing in the previous location. In the long run, these effects translate into an increased difference between the two groups of about 0.16 patents per inventor. Conversely, no city-wide spillover effect can be attested, offering little support to place-based policies aimed at inducing a positive influx of top innovators in urban areas.
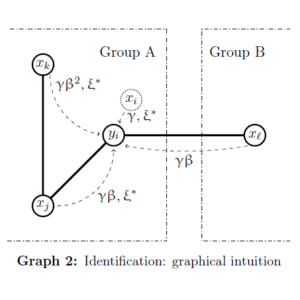Abstract. Conventional methods for the estimation of peer, social or network effects are invalid if individual unobservables and covariates correlate across observations. In this paper we characterize the identification conditions for consistently estimating all the parameters of a spatially autoregressive or linear-in-means model when the structure of social or peer effects is exogenous, but the observed and unobserved characteristics of agents are cross-correlated over some given metric space. We show that identification is possible if the network of social interactions is non-overlapping up to enough degrees of separation, and the spatial matrix that characterizes the co-dependence of individual unobservables and covariates is known up to a multiplicative constant. We propose a GMM approach for the estimation of the model’s parameters, and we evaluate its performance through Monte Carlo simulations. Finally, we show that in a typical empirical application about classmates our approach might estimate statistically non-significant peer effects when conventional approaches register them as significant